Implementing Santorini Bitboards with Haskell
0. Prerequisites
- Haskell: GHC version 8.10.x
- Libraries
- containers:
IntMapfor key-value pairs andSequencefor queues. - QuickCheck: For random instance generation.
- criterion: For benchmarking.
- containers:
1. Computing Player’s Moves
Problem Setting
Santorini is a turn-based strategy game for two players. The board consists of \(5 \times 5\) square spaces, and each space has a level from \(0\) to \(4\). Here is an excerpt from its basic rules.
- Each player owns two workers.
- On each turn, a player must move and then build with the selected worker.
- Any space at level \(4\) is capped; no worker can move or build there.
- A worker may move into one of the (up to) eight neighboring unoccupied spaces (like King’s movement in Western chess). A worker may:
- move up a maximum of one level higher
- move down any number of levels lower
- or move along the same level.
- A player can build a block on an unoccupied space neighboring the moved worker.
- If one of the workers moves up on top of level \(3\), the player wins.
Now, consider a program that computes of a worker’s all possible moves. For simplicity, We treat the spaces occupied by the other workers as level \(4\) so that a moving worker cannot reach any occupied spaces.
The signature of the function could be like this.
type Index = (Int, Int)
type Level = Int
getMoveTo :: (Index, [Level]) -> [Index]
getMoveTo (moveFrom, spaces) = ...
The Index consists of a pair of row and column indices (1-indexed). Any Level should be between \(0\) and \(4\), inclusive. The function getMoveTo() takes the following three arguments.
moveFrom: position of the selected worker- Example:
(1, 2)
- Example:
spaces: current level for each space, represented as a list for total \(25\) spaces \((1,1),(1,2),\ldots,(1,5),(2,1),\ldots(5,5)\).- Example:
[0,0,2,0,0,1,2,0,4,1,3,0,0,0,1,0,0,1,3,4,0,1,1,2,2]
- Example:
And we expect a result: [(1, 1), (2, 1), (2, 3)]
Naive Implementation
Here is an example straightforward implementation using list comprehension.
getMoveToNaive :: (Index, [Level]) -> [Index]
getMoveToNaive ((x, y), spaces) =
let levels = IntMap.fromList $ zip [0 ..] spaces
in [ (xx, yy)
| dx <- [-1, 0, 1],
dy <- [-1, 0, 1],
dx /= 0 || dy /= 0,
let xx = x + dx, -- move-to candidate
let yy = y + dy,
1 <= xx && xx <= 5, -- boundary check
1 <= yy && yy <= 5,
levels ! fromIndex (xx, yy) <= 3, -- cannot move up to level 4
levels ! fromIndex (x, y) + 1 >= levels ! fromIndex (xx, yy) -- can move up at most one level
]
But can we compute faster?
Implementing Bitboard
The idea of the bitboard is to represent each space as a bit (\(0\) or \(1\)) and the entire board as a bit array. There are \(25\) spaces on the board, but it is more convenient to have extra spaces around the boundary. We employ the following bitwise representation, which fits in a 64-bit integer. For example, space \((1,1)\) maps to index \(8\), and space \((1,2)\) to index \(9\), and in general, \((x,y)\) maps to \(7x+y\).
col 1 2 3 4 5
=============================
0 1 2 3 4 5 6
row --------------------
1 7 | 8 9 10 11 12| 13
2 14 |15 16 17 18 19| 20
3 21 |22 23 24 25 26| 27
4 28 |29 30 31 32 33| 34
5 35 |36 37 38 39 40| 41
--------------------
42 43 44 45 46 47 48
Notice that valid spaces are no longer from \(0\) to \(24\). We define \(V=\{7x + y \mid 1\leq x,y \leq 5\}\) as the set of valid indices. To represent a bitboard as an integer, we define the following function: \(b(X) = \sum_{i \in X} 2^i\). For instance, \(b(V) = 2147077824256\), which we can also represent as follows. In the diagram, - means \(0\) (bit off) and * means \(1\) (bit on).
-------
-*****-
-*****-
-*****-
-*****-
-*****-
-------
Here I would like to introduce several operations.
Neighborhood of an index
Let \(i\) be a valid index, and \(S=\{0, 1, 2, 7, 9, 14, 15, 16\}\), which is equivalent to the following diagram.
***----
*-*----
***----
-------
-------
-------
-------
Then, the bitboard of \(i\)’s neighborhood \(N(i)\) is given by bit shift and a few simple operations: \(N(i)=b^{-1}[\left(b(S)\ll(i-8)\right) \land b(V)]\).
getNeighborhood :: BBIndex -> BitBoard
getNeighborhood i = x `shift` (i + s) .&. globalMask
where
x = 115335 -- listToBB [0, 1, 2, 7, 9, 14, 15, 16]
s = -8
This effectively checks the board boundary. The following shows an example of \(N(19)\).
x:=
b(S) b(S)<<(19-8) x & b(V)
=b(S)<<11
***---- ------- -------
*-*---- ----*** ----**-
***---- ----*-* ----*--
------- ----*** ----**-
------- ------- -------
------- ------- -------
------- ------- -------
Closed neighborhood of a bitboard
We define the closed neighborhood of a set of spaces \(X\), denoted by \(N[X]\), as follows: \(N[X]=\bigcup_{x \in X}N[x]\), where \(N[x]=N(x) \cup \{x\}\). Then, \(N[X]\) can also be obtained by \(N[X]=b^{-1}[ ((x \ll 7) \lor x \lor (x \gg 7)) \land b(V))]\), where \(x = (b(X)\ll 1) \lor b(X) \lor (b(X)\gg 1)\).
getClosedNeighborhood :: BitBoard -> BitBoard
getClosedNeighborhood bb =
let x = bb .|. (bb `shift` 1) .|. (bb `shift` (-1))
y = x .|. (x `shift` 7) .|. (x `shift` (-7))
in y .&. globalMask
For \(N[\{8, 24, 25\}]\), computation would be like this.
z:= x:= y:= y & b(V)
b({8,24,25}) (z<<1)| (x<<7)|
z|(z>>1) x|(x>>7)
------- ------- ***---- -------
-*----- ***---- ***---- -**----
------- ------- ******- -*****-
---**-- --****- --****- --****-
------- ------- --****- --****-
------- ------- ------- -------
------- ------- ------- -------
Computing Move Range with Bitboard
Now, we can efficently compute the neighborhood of the given index. But how do we compare levels to determine whether or not a worker can move up? Luckily enough, levels are at most \(4\), and we can ignore level-\(4\) spaces as workers cannot move there anyways. So, we keep track of bitboards from level \(0\) to \(3\). Let \(L_k\) be a set of spaces whose level is \(k\). Here is an example.
Levels L_0 L_1 L_2 L_3
------- ------- ------- ------- -------
-00200- -**-**- ------- ---*--- -------
-12041- ---*--- -*---*- --*---- -------
-30001- --***-- -----*- ------- -*-----
-00134- -**---- ---*--- ------- ----*--
-01122- -*----- --**--- ----**- -------
------- ------- ------- ------- -------
By definition, all \(1\)-bits in \(L_k\) are distinct. The move-to range of a worker at index \(i\), denoted by \(M(i)\), can be computed as follows.
\[M(i) = \begin{cases} N(i) \land (L_0 \lor L_1) &\text{if }\ i \in L_0\\ N(i) \land (L_0 \lor L_1 \lor L_2) &\text{if }\ i \in L_1\\ N(i) \land (L_0 \lor L_1 \lor L_2 \lor L_3) &\text{if }\ i \in L_2 \lor L_3 \end{cases}\]This should be more efficient than checking the levels of \(i\)’s all neighbors. The following is an example implementation, along with the functions that convert input and output.
convertInput :: (Index, [Level]) -> (Int, [BitBoard])
convertInput (moveFrom, spaces) =
( toBBIndex moveFrom,
foldl'
( \[x0, x1, x2, x3] (i, y) ->
let bb = singletonBB i
in case y of
0 -> [x0 + bb, x1, x2, x3]
1 -> [x0, x1 + bb, x2, x3]
2 -> [x0, x1, x2 + bb, x3]
3 -> [x0, x1, x2, x3 + bb]
_ -> [x0, x1, x2, x3]
)
[0, 0, 0, 0]
(zip validIndices spaces)
)
convertOutput :: BitBoard -> [Index]
convertOutput = map fromBBIndex . bbToList
getMoveToWithBB :: (Index, [Level]) -> [Index]
getMoveToWithBB = convertOutput . getMoveToWithBB' . convertInput
getMoveToWithBB' :: (BBIndex, [BitBoard]) -> BitBoard
getMoveToWithBB' (i, [x0, x1, x2, x3]) = case getNeighborhood i of
nbr | i `elemBB` x0 -> nbr .&. (x0 .|. x1)
nbr | i `elemBB` x1 -> nbr .&. (x0 .|. x1 .|. x2)
nbr -> nbr .&. (x0 .|. x1 .|. x2 .|. x3)
getMoveToWithBB' _ = undefined
2. Computing All Distances
The biggest advantage of using bitboards is that we can perform (most) operations with a bitboard in constant time, regardless of the number of \(1\)-bits. Naturally, we want to compute the union of move ranges, that is: \(M(X)=\bigcup_{x \in X}M(x)\), where \(X\) is a set of spaces instead of a single index. It is not hard to see the following relationship.
\[\begin{aligned} M(X) =&(N[X] \cap L_0)\\ &\cup (N[X] \cap L_1)\\ &\cup (N[X \cap (L_1 \cup L_2 \cup L_3)] \cap L_2)\\ &\cup (N[X \cap (L_2 \cup L_3)] \cap L_3) \end{aligned}\]Here is an implementation. Note that \(b(L_1) \lor b(L_2) \lor b(L_3) = b(L_1) \oplus b(L_2) \oplus b(L_3) = b(L_0) \oplus b(L_1) \oplus b(L_2) \oplus b(L_3) \oplus b(L_0)\), where \(\oplus\) denotes exclusive or, because all \(1\)-bits are distinct among all levels.
getMoveToBB :: [BitBoard] -> [BitBoard] -> [BitBoard]
getMoveToBB [v0, v1, v2, v3] [x0, x1, x2, x3] =
let xx = x0 .|. x1 .|. x2 .|. x3
y0 = getClosedNeighborhood xx .&. v0
y1 = getClosedNeighborhood xx .&. v1
y2 = getClosedNeighborhood (xx `xor` x0) .&. v2
y3 = getClosedNeighborhood (x2 .|. x3) .&. v3
in [y0, y1, y2, y3]
getMoveToBB _ _ = undefined
Unfortunately, this function is not as fast as getMoveToWithBB' when a bitboard is singleton, that is, only one bit is on. However, if we consider the following problem, getMoveToBB can be advantageous.
Given an index \(i\), compute distances from \(i\) to all spaces.
The signagure would be:
getDistances :: (Index, [Level]) -> IntMap Int
getDistances (i, spaces) = ...
Here i is the starting index, and spaces holds level information. We expect key-value pairs where the key is the index of a space, normalized to the range from \(0\) to \(24\), and the value is the distance from \(i\). The distance from \(i\) to \(i\) itself is \(0\), and if a space is unreachable from \(i\), then the distance should be \(\infty\).
Naive BFS
This is so-called the single-source shortest path problem, and we could tackle this by BFS (breadth-first search). We use Data.Sequence for a queue because Data.List is not performant when an element is added to the last.
getDistancesNaive :: (Index, [Level]) -> IntMap Int
getDistancesNaive (moveFrom, spaces) =
let initMap = IntMap.fromList [(i, if i == fromIndex moveFrom then 0 else distInf) | i <- [0 .. 24]]
in getDistancesNaive' spaces (Seq.fromList [moveFrom]) initMap
getDistancesNaive' :: [Level] -> Seq Index -> IntMap Int -> IntMap Int
getDistancesNaive' spaces q sofar | Seq.null q = sofar
getDistancesNaive' spaces q sofar =
let x = q `Seq.index` 0
x' = fromIndex x
nbrs = getMoveToNaive (x, spaces)
unseen = Seq.fromList [nbr | nbr <- nbrs, (sofar ! fromIndex nbr) == distInf]
d = (sofar ! x') + 1
q' = Seq.drop 1 q Seq.>< unseen
sofar' = foldl (\m u -> IntMap.insert (fromIndex u) d m) sofar unseen
in getDistancesNaive' spaces q' sofar'
BFS with Bitboards
Here is the BFS code using getMoveToBB with bitboards.
getDistancesWithBB :: (Index, [Level]) -> IntMap Int
getDistancesWithBB i =
let (moveFrom, levels) = convertInput i
result = getDistancesWithBB' (singletonBB moveFrom) levels
result' = [((fromIndex . fromBBIndex) j, d) | (d, x) <- zip [0 ..] result, j <- bbToList x]
in IntMap.fromList $ zip [0 .. 24] (repeat distInf) ++ result'
getDistancesWithBB' :: BitBoard -> [BitBoard] -> [BitBoard]
getDistancesWithBB' moveFrom levels = (takeWhile (/= 0) . map (sum . fst)) $ iterate' f (map (.&. moveFrom) levels, moveFrom)
where
f (frontier, visited) =
let ys = getMoveToBB levels frontier
in (map (`andNotBB` visited) ys, visited .|. sum ys)
3. Benchmarking
We want to compare the performance between with and witout bitboards.
Generating Random Boards
First, we use QuickCheck to generate random instances. We add some biases to levels because we do not want too many spaces to be level \(4\).
import Test.QuickCheck (chooseInt, elements, generate, shuffle, vectorOf)
generateRandomInput :: Int -> IO [(Index, [Level])]
generateRandomInput n = generate $
vectorOf n $ do
indices <- shuffle [0 .. 24]
workerLevel <- chooseInt (0, 2)
emptyLevels <- vectorOf 21 $ elements [0, 0, 1, 1, 1, 2, 2, 2, 3, 4] -- levels at empty spaces
let spaces = (map snd . sort . zip indices) (workerLevel : [4, 4, 4] ++ emptyLevels)
let worker = toIndex $head indices
return (worker, spaces)
Benchmark Code
We use criterion for benchmarking. See the tutorial for details.
We test the getMoveTo functions with \(10^5\) instances, and getDistances with \(10^4\) instances. We also check if those functions return exactly the same value.
import Criterion.Main (bench, bgroup, defaultMain, nf)
verify :: (Index, [Level]) -> Bool
verify x = getMoveToNaive x == getMoveToWithBB x && getDistancesNaive x == getDistancesWithBB x
main :: IO ()
main = do
instances <- generateRandomInput 100000
let instances' = map convertInput instances
-- check correctness
guard $ all verify instances
-- benchmark
defaultMain
[ bgroup
"getMoveTo"
[ bench "Naive" $ nf (map getMoveToNaive) instances,
bench "BB" $ nf (map getMoveToWithBB) instances,
bench "BB (core)" $ nf (map getMoveToWithBB') instances'
],
bgroup
"getDistances"
[ bench "Naive" $ nf (map getDistancesNaive) (take 10000 instances),
bench "BB" $ nf (map getDistancesWithBB) (take 10000 instances)
]
]
The benchmark BB (core) measures only the core logic without input and output conversions.
Benchmark Result
As we expected, using bitboards improved the overall performance for both problems. If we compare core logic, getMoveToWithBB is 20 times faster than the naive implementation. As for computing distances, getDistancesWithBB is around five times faster than the naive one.
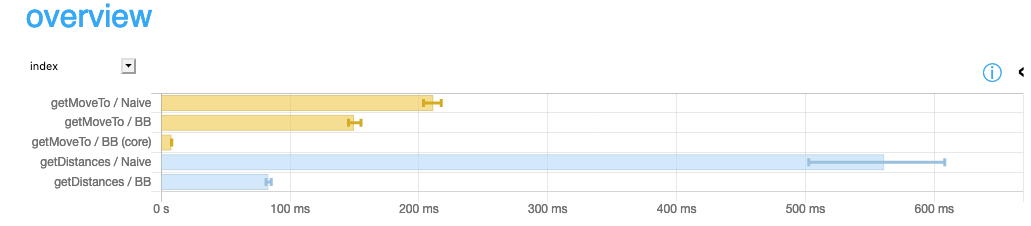
benchmarking getMoveTo/Naive
time 201.3 ms (190.9 ms .. 221.3 ms)
0.994 R² (0.969 R² .. 1.000 R²)
mean 211.2 ms (203.5 ms .. 217.3 ms)
std dev 8.909 ms (6.801 ms .. 11.81 ms)
variance introduced by outliers: 14% (moderately inflated)
benchmarking getMoveTo/BB
time 154.8 ms (144.8 ms .. 166.7 ms)
0.993 R² (0.975 R² .. 1.000 R²)
mean 149.6 ms (145.3 ms .. 154.9 ms)
std dev 7.277 ms (5.587 ms .. 8.660 ms)
variance introduced by outliers: 12% (moderately inflated)
benchmarking getMoveTo/BB (core)
time 8.066 ms (7.902 ms .. 8.234 ms)
0.996 R² (0.993 R² .. 0.998 R²)
mean 7.967 ms (7.861 ms .. 8.100 ms)
std dev 336.1 μs (251.3 μs .. 483.2 μs)
variance introduced by outliers: 19% (moderately inflated)
benchmarking getDistances/Naive
time 446.4 ms (159.1 ms .. 618.8 ms)
0.956 R² (0.851 R² .. 1.000 R²)
mean 561.1 ms (502.6 ms .. 608.0 ms)
std dev 61.83 ms (10.67 ms .. 84.72 ms)
variance introduced by outliers: 23% (moderately inflated)
benchmarking getDistances/BB
time 86.04 ms (82.47 ms .. 91.98 ms)
0.993 R² (0.983 R² .. 0.999 R²)
mean 83.13 ms (81.23 ms .. 85.34 ms)
std dev 3.896 ms (2.993 ms .. 5.197 ms)
See the full report for more details.
4. Code
- Repository: https://github.com/mogproject/santorini-bitboard-example
- Algorithms: BenchMain.hs
- BitBoard: BitBoard.hs