Level Sets
We propose to use level-set based implicit models to represent surface shape.
Osher &
Sethian
A curve can be thought of as a level set of some discretely
sampled 2D function.

|
showed how
deformation could be modeled on discrete grids using level sets.
Level-set models possess several
advantages over conventional parametric models. The models are topologically
flexible, and can split and rejoin as necessary in the course of deformation
without the need for re-parametrization. The model can be thought of as the
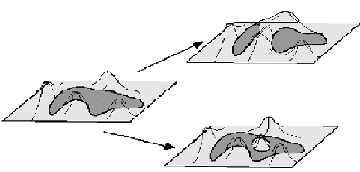
level set of a surface, for instance a lake shore as depicted here.
Changing the surface moves the boundary of the model, as changing the terrain
would move the boundary of the lake shown here.
The evolution of the level-set function is independent of translation,
rotation, and arbitrary decisions regarding parametrization. The resulting
shapes are solely dependent on the resolution of the voxels used to represent
the function, and not on some basis function. Finally, multi-scale solutions
are possible, allowing the model to start on a coarse
The model can also be thought
of as the level set of a surface, i.e. a lake shore.
|
grid and progress on finer grids until a solution is reached. This not only reduces
computation time, but also controls the relative importance of different
sized structures in the model. One of several
examples of level sets in
computer graphics is morphing from one shape to another.
For a more in-depth explanation of level sets see Dr. J. A.
Sethian's
informative page on the subject.
Further information is also available from the UCLA
Computational and Applied Mathematics group.
Contact amangan@utk.edu


