Fast Approximation of Convex Hull

Ladislav Kavan
FEE CTU in Prague
 
Ivana Kolingerova
University of West Bohemia
 
Jiří Žára
FEE CTU in Prague
 


a) An example of BCH10 that does not contain all points of the input set. b) Already BCH12 contains all points of the input set. However there is a small redundancy over the accurate convex hull.


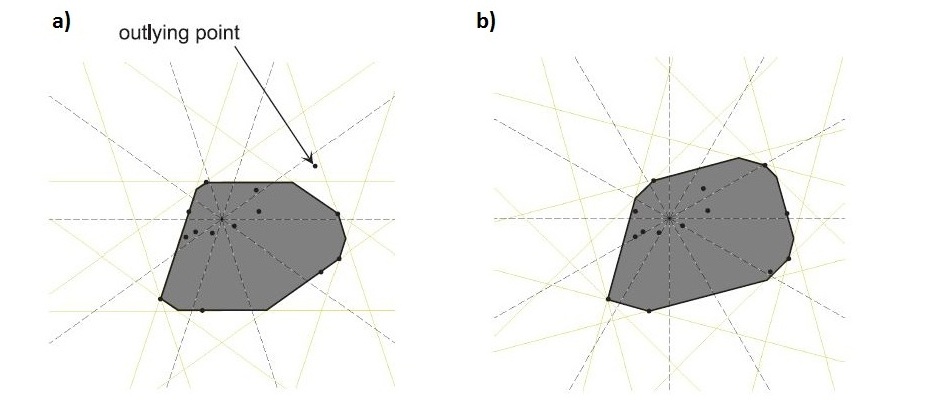
Abstract

The construction of a planar convex hull is an essential operation in computational geometry. It has been peroven that the time complexity of an exact solution is Nlog(N). In this paper, we describe an algorithm with time complexity O(N+k^2), where k is parameter controlling the approximation quality. This is beneficial for applications processing a large number of points without necessity of an exact solution. A formula for upper bound of the approximation error is presented.


Publication

Ladislav Kavan, Ivana Kolingerova, Jiří Žára. Fast Approximation of Convex Hull. Advances in Computer Science and Technology, 2006.  

Links and Downloads

Paper

 
BibTeX


Acknowledgements

This work has been partly supported by the Ministry of Education, Youth and Sports of the Czech Republic under research program MSM 6840770014 (Research in the Area of the Prospective Information and Navigation Technologies).