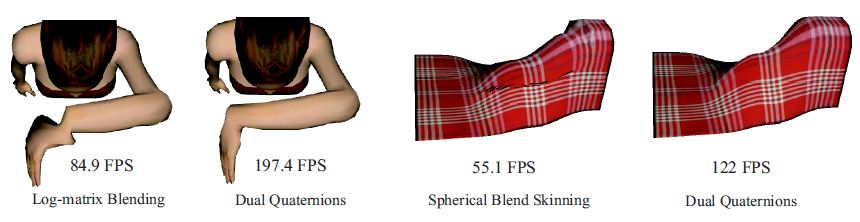
Dual Quaternions for Rigid Transformation Blending
A comparison of different rigid transformation blending algorithms applied in skinning shows that blending based on dual quaternions not only eliminates artifacts, but is also much easier to implement and more than twice as fast as previous methods.
AbstractQuaternions have been a popular tool in 3D computer graphics for
more than 20 years. However, classical quaternions are restricted
to the representation of rotations, whereas in graphical applications
we typically work with rotation composed with translation (i.e., a
rigid transformation). Dual quaternions represent rigid transformations
in the same way as classical quaternions represent rotations.
In this paper we show how to generalize established techniques for
blending of rotations to include all rigid transformations. Algorithms
based on dual quaternions are computationally more efficient
than previous solutions and have better properties (constant
speed, shortest path and coordinate invariance). For the specific example
of skinning, we demonstrate that problems which required
considerable research effort recently are trivial to solve using our
dual quaternion formulation. However, skinning is only one application
of dual quaternions, so several further promising research
directions are suggested in the paper.
PublicationLadislav Kavan, Steven Collins, Carol O'Sullivan, Jiří Žára. Dual Quaternions for Rigid Transformation Blending. Technical Report, Trinity College Dublin, 2006.  
Links and DownloadsPaper
 | | BibTeX
 |
 |
|