
|
A Static Priority Analysis Kit
|
Summary
SPAK implements a number of response time analyses for real-time task
sets scheduled using fixed priorities with preemptive scheduling,
non-preemptive scheduling, and with mixed preemption relations. It
also includes many functions for manipulating task set parameters and
optimizing various task set characteristics, as well as a simulator
for testing the execution of task sets.
Download
SPAK is distributed under a BSD-style license.
spak-0.3.tar.gz -- 5/24/02
SPAK is regularly tested on Linux, FreeBSD, and Cygwin. However,
since it requires only very generic system services it should compile
on almost any Unix-like platform. CFLAGS will have to be changed if a
compiler other than gcc is used. Compiling with Visual C++ is easy if
you load the SPAK sources into a fresh "Win32 console
application."
To make graphical execution traces from simulation runs, SPAK requires
Jgraph
to be installed.
Documentation
Currently the best "documentation" is the examples and source code
below, and the SPAK source itself. Cleaning up the SPAK API and
documenting it is on my short list of things to do.
A recent paper that I wrote used SPAK
to generate all experimental data. The paper does not go into any
detail about SPAK or how to use it, but it should give an idea of
SPAK's capabilities.
Example 1 : Finding a Feasible Schedule
One of the simplest uses of SPAK is to find a feasible schedule for a
task set. SPAK knows how to analyze task sets that are fully
preemptive, fully non-preemptive, and those that mix preemption and
non-preemption.
Consider this task set, which is from a paper about preemption
threshold scheduling by Wang and
Saksena:
t0 : C=20, T=70, D=50
t1 : C=20, T=80, D=80
t2 : C=35, T=200, D=100
This SPAK program attempts to find a
feasible schedule for the task set using preemptive scheduling,
non-preemptive scheduling, and preemption threshold scheduling. When
run it produces the following output:
optimal preemptive algorithm did not find a schedule
optimal non-preemptive algorithm did not find a schedule
found a schedule using preemption thresholds:
task set preemption_thresh_rtcsa_table1
parameters Tclk 1000 Cclk 0 Cql 0 Cqs 0
Task Name C T D J U P PT S R Thr
t1 20 70 50 0 0.28571 0 0 1 39 -1
t2 20 80 80 0 0.25000 2 0 1 75 -1
t3 35 200 100 0 0.17500 1 1 1 94 -1
This is basically what Wang and Saksena say in their paper, although
they use high numeric values to indicate high priorities and
preemption thresholds, while SPAK uses low values to indicate high
priorities and preemption thresholds.
The file apps/examples/example_1.c in the SPAK distribution
contains the code for this example.
Example 2 : Analyzing the Robustness of Schedules
A timing fault occurs when a real-time task produces the
correct result later than it should have. It can be extremely
difficult to produce real-time systems that are provably free of
timing faults, and some of the most
convincing stories about worst-case execution time (WCET) analysis
are statistical in nature. In the paper above, we explore the idea
that when there is generic uncertainty about task WCET, task sets with
high critical scaling factors are to be preferred over other
feasible schedules. The critical scaling factor is the largest number
by which the WCET of each task in a set can be multiplied without
rendering the task set infeasible.
Consider the following task set:
t0 : C=400 ; T,D=1999 ; J=0
t1 : C=400 ; T,D=2000 ; J=1200
This SPAK program analyzes two feasible
schedules for this task set: the deadline-monotonic schedule, and the
schedule that has the highest critical scaling factor. These are, in
fact, the only two possible fully preemptive schedules.
SPAK also runs its built-in task simulator on each of the schedules in
order to experimentally test its behavior during timing faults. These
runs result in two data files "dm.dat" and "robust.dat". Typing
plot "dm.dat", "robust.dat"
in
Gnuplot creates a graph similar to this one:
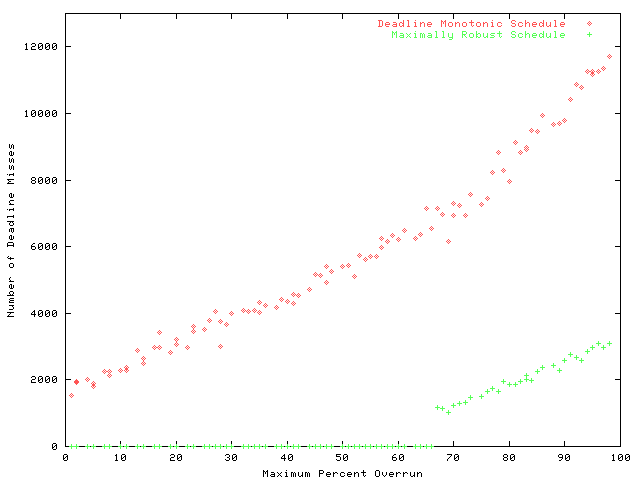
All other factors being equal, the "robust" schedule is clearly
preferable if the possibility of timing faults has not been ruled
out. Section 4 of the paper above goes into a lot more detail on
this subject.
The file apps/examples/example_2.c in the SPAK distribution
contains the code for this example.
Example 3 : Finding Out Why Deadlines Are Missed
By definition a task set is feasible if no task has a worst-case
response time larger than its deadline, and infeasible otherwise.
However, since the response time of a task is a non-linear function of
the characteristics of all higher-priority tasks, the story that
response times tell the real-time system developer can leave something
to be desired in terms of understanding the underlying problem.
This SPAK program creates an example task set,
assigns priorities in deadline monotonic fashion, computes that this
schedule is infeasible, and then simulates the execution of the task
set. When run, it prints the following to STDOUT:
task set audsley93_t3
parameters Tclk 1000 Cclk 0 Cql 0 Cqs 0
Task Name C T D J U P PT S R Thr
t1 3500 200000 5000 0 0.01750 0 0 1 3500 -1
t2 2000 25000 25000 0 0.08000 1 1 1 5500 -1
t3 5000 25000 25000 0 0.20000 2 2 1 10500 -1
t4 1000 40000 40000 0 0.02500 3 3 1 11500 -1
t5 9000 50000 50000 0 0.18000 4 4 1 20500 -1
t6 5000 50000 50000 0 0.10000 5 5 1 32500 -1
t7 8000 59000 59000 0 0.13559 6 6 1 41500 -1
t8 12000 80000 80000 0 0.15000 7 7 0 90500 -1
t9 2000 80000 80000 0 0.02500 8 8 0 141500 -1
task set is not feasible
simulation results:
t1 max resp time: analytic 3500, sim 3500 (at 3500) (off by 0) (498 times)
t2 max resp time: analytic 5500, sim 5500 (at 5500) (off by 0) (85 times)
t3 max resp time: analytic 10500, sim 10500 (at 10500) (off by 0) (46 times)
t4 max resp time: analytic 11500, sim 11500 (at 11500) (off by 0) (14 times)
t5 max resp time: analytic 20500, sim 20500 (at 20500) (off by 0) (151 times)
t6 max resp time: analytic 32500, sim 32500 (at 32500) (off by 0) (79 times)
t7 max resp time: analytic 41500, sim 41500 (at 41500) (off by 0) (1 times)
t8 max resp time: analytic 90500, sim 90500 (at 90500) (off by 0) (4 times)
t9 max resp time: analytic 141500, sim 141500 (at 141500) (off by 0) (9 times)
The simulation corroborates the response time analysis: at least one
simulated instance of each task reached its maximum response time
during the run.
Now assume that we're interested in seeing the chain of events that
caused task 8 to miss its deadline. The SPAK run above produced, in
addition to some screen output, a trace of the simulated task
execution. Running the command
../scripts/render_sim_output.pl sim_output.txt 0 100000
creates a graph depicting the first 100,000 time units of the
simulation:
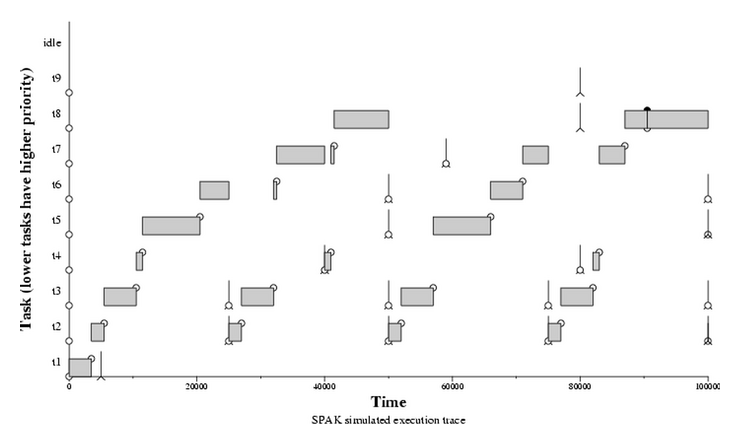
This picture follows conventions established by the STRESS
simulator: open circles at the bottom are task releases, up arrows are
deadlines, open circles at the top are on-time completions of task
instances, and closed circles are missed deadlines. Notice that task
8 misses a deadline around time 90,000. There is no idle time before
the deadline miss (simulation time zero is a critical instant); there
is simply not enough CPU time to permit tasks 8 and 9 to run on time.
This SPAK program uses the response time
analysis to tell the developer by what amount the WCET of each task
(taken individually) would need to be scaled to make an infeasible
task set feasible. It produces the following output:
task 0 : no scaling of this task can make the set feasible!
task 1 : no scaling of this task can make the set feasible!
task 2 : WCET must be scaled by 0.450000 to make the set feasible
task 3 : no scaling of this task can make the set feasible!
task 4 : WCET must be scaled by 0.472000 to make the set feasible
task 5 : WCET must be scaled by 0.050000 to make the set feasible
task 6 : WCET must be scaled by 0.406000 to make the set feasible
task 7 : WCET must be scaled by 0.541000 to make the set feasible
task 8 : no scaling of this task can make the set feasible!
task 9 : no scaling of this task can make the set feasible!
Since the deadline monotonic scheduling algorithm is optimal for this
task set (it has no tasks with jitter, and all deadlines are less than
or equal to periods), we can only conclude that the designers of this
system are in trouble! Perhaps they need to invest in a faster
processor or a WCET analyzer that gives tighter bounds.
The file apps/examples/example_3.c in the SPAK distribution
contains the code for this example.
regehr@cs.utah.edu
Glenn Wasson developed the SPAK logo in an entirely
different context. However, since I earned most (or all, if you
belive Glenn's web page...) of the actual spaks, I felt justified in
stealing it.
Check out some of the other
SPAKs that can be found on the net.



