CS 2010 Homework 11   - Due November 6

Setup

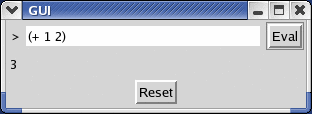
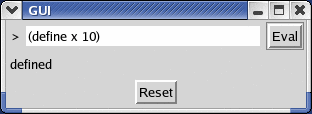
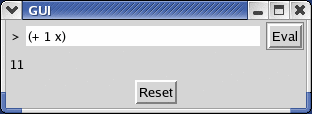
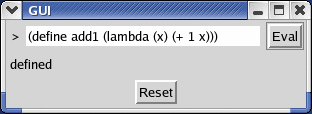
The HW 11 setup is the same as for HW 10, and this assignment builds on your HW 10 solution.

Assignment

Exercise 11.1, Expressions

We revise three data definitions from HW 10, and add a few more:

 ;;  A defn-snl is
 ;;   (list 'define sym expr-snl)
 ;;   (list 'define sym (list 'lambda (list sym) expr-snl))
 ;; 
 ;;  A assign-snl is
 ;;   (list 'set! sym expr-snl)
 ;; 
 ;;  An expr-snl is either
 ;;   - sym
 ;;   - num
 ;;   - plus-expr-snl
 ;;   - minus-expr-snl
 ;;   - times-expr-snl
 ;;   - app-expr-snl
 ;;
 ;; A plus-expr-snl is
 ;;  (list '+ expr-snl expr-snl)
 ;;
 ;; A minus-expr-snl is
 ;;  (list '- expr-snl expr-snl)
 ;;
 ;; A times-expr-snl is
 ;;  (list '* expr-snl expr-snl)
 ;;
 ;; An app-expr-snl is
 ;;  (list sym expr-snl)
 ;;
 ;; A func is
 ;;   (make-func sym expr)
 (define-struct func (name body))

Thus, a definition is now a number or function defition, and an expression is either a variable, a number, an addition, a subtraction, a multiplication, or a function call.

Based on the new data definitions, revise your implementation of the following functions:

  ; is-defn? : snl -> bool
  ;  Returns true if s is a defn-snl
  (define (is-defn? s) ...)

  ; is-assign? : snl -> bool
  ;  Returns true if s is an assign-snl
  (define (is-assign? s) ...)

  is-expr? : snl -> bool
  ;  Returns true if s is a expr-snl
  (define (is-expr? s) ...)

  ; add-definition : sym num-or-func -> string
  (define (add-definition s v) ...)

  ; get-value : sym -> num-or-func-or-false
  (define (get-value s) ...)

Note that, based on the shape of the data definitions, you will need to write is-plus?, etc., as well.

Exercise 11.2, Substitution

Evaluation of function calls will require substitution, which takes an expression representing the function body, a variable for the function argument, and a value to replace the variable in the body:

   substitute : expr-snl sym num -> expr-snl

Implement substitute.

Some examples (incomplete set):

(substitute '(+ x 7) 'x 12) "should be" '(+ 12 7)
(substitute 'x 'x 12) "should be" 12
(substitute 'y 'x 12) "should be" 'y

Exercise 11.3, Evaluation

Implement evaluate, which takes an expression and produces its value (a number). Obtain a value for a variable expression or function call using get-value (which consults the table of definitions).

Evaluation can fail for many reasons, such as using a function name as an expression, or using a variable with no definition. At this point, the result of evaluate for erroneous expressions can be undefined.

Examples:

   (evaluate '(+ 1 2)) "should be" 3
   (clear-definitions)
   (add-definition 'f (make-func 'x '(+ x 1)))
   (evaluate '(f 4)) "should be" 5
   (add-definition 'x 9)
   (evaluate 'x) "should be" 9
   (add-definition 'g (make-func 'y '(+ x y)))
   (evaluate '(g 10)) "should be" 19

Exercise 11.4, Execution with Expressions

Change execute to work with the revised defn-snl, assign-snl, and expr-snl. In particular:

• Executing a function definition registers a function name.
• Executing a non-function definition or an assignment involves evaluating an expression to get a value for the definition or assignment.
• Executing a expr-snl requires evaluating it.

At this point, your GUI should be able to evaluate expressions.

Exercise 11.5, OPTIONAL: Dealing with Errors

Change evaluate so that it produces either a value or a string, where a string represents an evaluation error. When evaluating a sub-expression (e.g., for an addition), if the result is an error string, then the result of the whole expression should be an error string.

Use this error string for the result of an execution. When evaluating the expression in a definition or assignment, perform no definition or assignment if the evaluation result is an error, and instead return the error string.

Exercise 11.6, OPTIONAL: Conditionals

More data-definition adjustments:

 ;;  An expr-snl is either
 ;;   - sym
 ;;   - num
 ;;   - plus-expr-snl
 ;;   - minus-expr-snl
 ;;   - times-expr-snl
 ;;   - app-expr-snl
 ;;   - cond0-expr-snl
 ;;
 ;;  A cond0-expr-snl is
 ;;   (list 'cond0 (list expr-snl expr-snl) (list 'else expr-snl))

To evaluate acond0-expr-snl, evaluate the first sub-expression. If that result is 0, then the result for the whole cond0-expr-snl is the result of the second sub-expression, and the third expression is never evaluated. If the result for the first expression is not 0, then the result for the whole cond0-expr-snl is the result of the third sub-expression.

You can now implement and execute, say, the factorial function in your DrScheme.