Shared Memory & Network Models
story thus far …
four step design methodology
message passing interface
minimal set of six MPI functions we will need
// Initiates use of MPI
int MPI_Init(int *argc, char ***argv);
// Concludes use of MPI
int MPI_Finalize(void);
// On return, size contains number of processes in comm
int MPI_Comm_size(MPI_Comm comm, int *size);
// On return, rank contains rank of calling process in comm
int MPI_Comm_rank(MPI_Comm comm, int *rank);
// On return, msg can be reused immediately
int MPI_Send(void *msg, int count, MPI_Datatype datatype,
int dest, int tag, MPI_Comm comm);
// On return, msg contains requested message
int MPI_Recv(void *msg, int count, MPI_Datatype datatype,
int source, int tag, MPI_Comm comm, MPI_Status *status);
example: reduction
Given \(A\in\mathbb{R}^n\), compute \(\sum_{i=1}^n A_i\)
// option 1
double sum1(double *A, int n) { // W D
double sum=0.0; // 1 1
for (i=0; i<n; ++i) sum += A[i]; // n n
return sum; // 1 1
}\[ W(n) = 2 + n, \quad D(n) = 2 + n, \quad P(n) = \mathcal{O}(1) \]
// option 2
double sum2(double *A, int n) { // W D
if (n == 1) return A[0]; // 1 1
parallel for (i=0; i<n/2; ++i) // n 1
B[i] = A[2i] + A[2i+1];
return sum2 (B, n/2); } // W(n/2) D(n/2)\[ W(n) = n + W(n/2), \quad D(n) = 1 + D(n/2), \quad P(n) = \mathcal{O}(n/\log n) \]
today
- PRAM
- Network Models
- Collective communications
PRAM
- parallel random access memory
- shared memory model (synchronous)
- SIMD - specify code for single thread
- same instruction for all threads
- no memory access cost
- each thread has its own memory along with shared memory
- shared memory variables must be declared
- global/local memory (read/write)
- ER/CR: exclusive read, concurrent read
- EW/CW: exclusive write, concurrent write
- CREW PRAM: most practical
- Complexity estimates: \(T(n,p), W(n,p)\)
PRAM sum
# t: thread id, p: number of threads (n,p: power of two)
PRAM_sum(A,n):
if n > p:
r = n/p
w = SEQ_sum (A[tr], r)
S[t] = global_write (w) # EW
return PRAM_sum (S, p)
if t <= n/2:
a1 = global_read (A[2t]) # ER
a2 = global_read (A[2t+1]) # ER
S[t] = global_write(a1+a2) # EW
return PRAM_sum (S, p/2)PRAM MATVEC
PRAM MATVEC
\(A\) is \(n \times n\), \(x\)(input), \(y\)(output) : in global memory
# assume n>p, n%p == 0
PRAM_matvec(A, x, y, n):
r = n/p
z = global_read (x) # CR - O(n)
B = global_read (A[tr, :], r) # ER - O(n^2/p)
w = SEQ_matvec (B, z) # W = O(n^2/p)
y[tr, (t+1)r] = global_write (w) # EW - O(n/p)scheduling DAGs to PRAM
- scheduling principle: \(T(n,p) \leq \lfloor W(n)/p \rfloor + D(n)\)
- simulate work at \(i_{th}\)—\(W_i(n)\) level using \(p\) processors
- total runtime
\[ \begin{align} T(n,p) & \leq \sum_i \left\lceil\frac{W_i(n)}{p}\right\rceil \\ & \leq \sum_i \left(\left\lfloor\frac{W_i(n)}{p}\right\rfloor + 1 \right) \\ & \leq \left\lfloor\frac{W(n)}{p}\right\rfloor + D(n) \end{align} \]
network models
message passing model
network topologies
- Access to remote data requires communication
- Direct connections would require \(\mathcal{O}(p^2)\) wires and communication ports, which is infeasible for large \(p\)
- Limited connectivity necessitates routing data through intermediate processors or switches
- Topology of network affects algorithm design, implementation, and performance
common network topologies
common network topologies
message passing
\(T_{msg} = t_s + t_w L\)
- \(t_s\) = startup time = latency (i.e., time to send message of length zero)
- \(t_w\) = incremental transfer time per word (\(1/t_w\) = bandwidth in words per unit time)
- \(L\) = length of message in words
For most real parallel systems, \(ts \gg tw\)
cost of collectives
reduction
ring reduction pseudocode
reduction(A, id, p) { s=A for k=0:log2(p)-1 { r = 2^k; cid = id/r; if ~isInt(cid) break; end if even(cid) { partner = (cid+1)*r; recv (sp, partner); s=s+sp; } else { partner = (cid-1)*r; send(s, partner); } } return s; }hypercube
hypercube reduction
hypercube reduction
hypercube reduction
hypercube reduction
hypercube reduction
hcube_reduction(A, id, p) { d = log2(p); s = A; mask = 0; for k=0:d-1 { r = 2^k; // run only if id's lower k bits == 0 if id & mask == 0 { partner = id ^ r; // flip the kth bit if id & r { send(s, partner); } else { recv(sp, partner); s = s + sp; } } mask = mask ^ r; % lower k bits = 1 } }broadcast
source node sends the same message to each of \(p-1\) other nodes
int MPI_Bcast (void* buffer, int count, MPI_Datatype datatype, int root, MPI_Comm comm);broadcast
broadcast
Cost of broadcast depends on network, for example
————|—————————— 1-D mesh | \(T=(p-1)(t_s + t_wL)\) 2-D mesh | \(T=2(\sqrt{p}-1)(t_s + t_wL)\) hypercube | \(T=\log p (t_s + t_wL)\)
scatter & gather
int MPI_Gather(void* sbuf, int scount, MPI_Datatype stype, void* rbuf, int rcount, MPI_Datatype rtype, int root, MPI_Comm comm ) int MPI_Scatter(void* sbuf, int scount, MPI_Datatype stype, void* rbuf, int rcount, MPI_Datatype rtype, int root, MPI_Comm comm)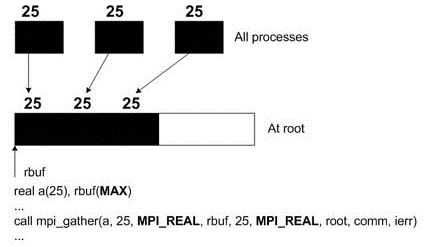
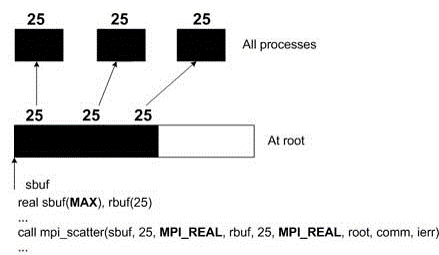
scatter & gather
int MPI_Gather(void* sbuf, int scount, MPI_Datatype stype, void* rbuf, int rcount, MPI_Datatype rtype, int root, MPI_Comm comm ) int MPI_Scatter(void* sbuf, int scount, MPI_Datatype stype, void* rbuf, int rcount, MPI_Datatype rtype, int root, MPI_Comm comm)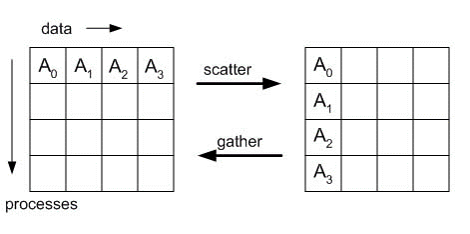
allgather
int MPI_Allgather(void* sbuf, int scount, MPI_Datatype stype, void* rbuf, int rcount, MPI_Datatype rtype, MPI_Comm comm)
all to all
int MPI_Alltoall(void* sbuf, int scount, MPI_Datatype stype, void* rbuf, int rcount, MPI_Datatype rtype, MPI_Comm comm)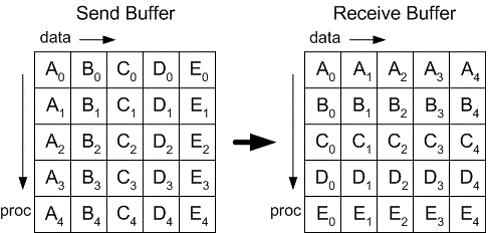
scan, prefix sum
- Given an array, \([4, 2, 1, 8]\)
- Compute, \([4, 4+2, 4+2+1, 4+2+1+8]\)
- \([4, 6, 7, 15]\)
obvious sequential algorithm
\[ D_s(n) = (n) \]
not parallelizable, need to change algorithm
recursive scan
s = Rec_Scan(a,n) // s[k]= a[0]+a[1]+…+a[k-1], k=0,…,n-1 1. if n=1 { s[0]←a[0]; return; } //base case 2. par for (i=0; i<n/2; ++i) b[i] ← a[2i] + a[2i+1]; 3. c ← Rec_Scan (b, n/2); 4. s[0] ← a[0]; 5. par for (i=0; i<n; ++i) if isOdd(i) s[i] ← c[i/2]; else if isEven(i) s[i] ← c[i/2] + a[i];reading
Intro to Parallel Algorithms
first chapter of Jájá’s book.












